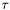 is attached to this time quantity. Within the Quantities package, names and symbols of quantities should have some reasonably defined default value, which might be overwritten by the user when generating a quantity, or at some later stage.
is attached to this time quantity. Within the Quantities package, names and symbols of quantities should have some reasonably defined default value, which might be overwritten by the user when generating a quantity, or at some later stage.Quantities package is that of a quantity. A quantity is an entity which is composed of a (numerical) value and a unit (see below, Unit), and related to other quantities by a dimension (see below, Dimension). In science and other fields of research, quantities are used to describe some "attribute of a phenomenon, body or substance" [McNaught/Wilkinson_1997] in a quantitative way. For example, time is a particular quantity. If we perform calculations with quantities, we are engaged in quantity calculus [White_1998].
Apart from the numerical value, the dimension, and the unit in which the value is given, a scientist will often qualify a quantity by a name and/or a symbol, which denote its use in a given context. For example, in electroanalytical chemistry, when defining a cyclic voltammetric experiment, the time needed to scan the potential of the electrode from its starting value to the value when its direction is reversed is called the `switching time' (name), and, conventionally, the symbol 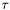 is attached to this time quantity. Within the Quantities package, names and symbols of quantities should have some reasonably defined default value, which might be overwritten by the user when generating a quantity, or at some later stage.
is attached to this time quantity. Within the Quantities package, names and symbols of quantities should have some reasonably defined default value, which might be overwritten by the user when generating a quantity, or at some later stage.
It will turn out advantageously to group quantities together according to some of their basic properties: among others the dimension and the list of units which can be used with the quantity. Such quantities belonging to the same quantity type may differ for example in the particular unit in which the numerical value is measured, or in the way the numerical value is expressed (e.g., with or without a decimal point).
Although the SI (Système International d'Unités) provides only a single unit for a particular quantity, quite often several units for this quantity are in practical use. For example, time is not only measured in seconds but also in minutes (min). Some units [e.g., millisecond (ms)] contain a prefix. There is a limited list of prefixes, which define multiples of 10 of the underlying unit. Thus, each quantity has associated with it a non-empty list of units, which it has available for use when performing quantity calculus.
Conceptually, we distinguish four types of units:
In quantity calculus, the quantity represents the product of the value and the attached unit. The value of a quantity can be recalculated to be measured in any of its units. This will be called "to recalculate the quantity from one of the units in terms of another (appropriate) unit", a transformation which is also called conversion.
As an additional feature, we will provide units with a name and a symbol for easy identification.
The SI defines seven SI base units (corresponding to the seven SI base quantities): metre, kilogram, second, ampere, kelvin, mole, and\ candela. Moreover, each other quantity is denoted a SI derived quantity and is related to one or more of the base quantities by an algebraic expression devised by multiplying and/or dividing powers of the base quantities. The dimension of a (SI base or derived) quantity is given by the exponents of the seven SI base quantities in the expression. In general, only rational exponents will be encountered. We will call these seven numbers the components of a quantity's dimension. The dimension is an ordered septuple of such rational numbers.
If all seven components are zero, we call the quantity dimensionless.
For example, the SI derived quantity area (symbol  ) is related to the SI base quantity length (symbol
) is related to the SI base quantity length (symbol 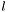 ) by
) by 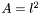 . Thus, the length exponent is 2, while all other six exponents are equal to 0. The dimension of the area quantity will thus be
. Thus, the length exponent is 2, while all other six exponents are equal to 0. The dimension of the area quantity will thus be 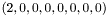 .
.
The dimension of a quantity is important in quantity calculus to define commensurability (commensurable: ``having a common measure'' [Webster_1993]). Two quantities are regarded commensurable if their dimensions are identical, i.e. all the dimension components are identical. This use of the term in our context is slightly different from its definition in Wikipedia [Commensurability_Wikipedia], where the measurement `in the same units' is stressed. This would prevent the use of `artificial' quantities within Quantities, which do have a defined dimension but do not have one of the SI units at all (generated quantities, see below). However, since one common unit between all quantities with a certain dimension could be constructed from the respective base quantities raised to the power of the dimension component, our use is at least consistent with the definition of commensurability through units.
Only commensurable quantities can be assigned to each other in a calculation. For example, a product of two lengths has the dimension of an area and can be assigned to an area quantity. However, it can not be assigned to a time quantity. For non-commensurable quantities also some other operations are illegal (see below).
Moreover, `dimensional analysis' [BoostMPL], [BartonNackman_1994](section 16.5) deals only with a partial aspect of quantity calculus: the representation, manipulation, and compile time checking of the dimension. While it is indeed important to derive the dimension of any quantity that can be generated by arithmetical calculation, in particular multiplication and division, from other quantities, as shown above, the approaches cited do not directly support the unit concept independently.
For each base quantity, however, there may be several sub-types, which have the same characteristic features, but differ in some other respect. For example, among electric charge quantities we might have variable or constant values. Moreover, we might have special electric charge quantities, which have fixed values in every context, for example, the electron and the proton charge. All the electric charge quantities share the dimension of electric charge and the units in which the values can be expressed. We will call such sub-types of quantities derived quantities (again not to be confused with the concept of SI derived quantities).
A quantity may have various modes of accessibility. This will influence its use.
... storage type ... storage unit ...
... Dynamic ... Generated ...
A quantity will be realized a C++ object.
Conversions might be realized as copy (see above) or assignment (see below) operations.
=.
Addition (common symbol: 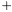 ) and multiplication (common symbol:
) and multiplication (common symbol: 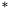 or
or  or
or  ) are commutative operations. The two operands in an addition operation must be commensurable. The same is true for subtraction. On the other hand, no restriction is placed on the operands of multiplication and division operations in terms of commensurability.
) are commutative operations. The two operands in an addition operation must be commensurable. The same is true for subtraction. On the other hand, no restriction is placed on the operands of multiplication and division operations in terms of commensurability.
... other arithmetical operations ...
Unary + and - operations work on the sign of a quantity, either leaving it as it is or changing it into the opposite. As a result, unary + does not change its operand at all. It was added to the ANSI C standard as a symmetry complement to unary - [Kernighan/Ritchie_1988] p. 204.
Increment and decrement operations should be designed in analogy to the predefined counterparts for for built-in types. Thus, prefix and postfix variants are considered. All these operations change the value of the quantity object. Consequently, only variable forms of a quantity can be incremented or decremented, and these operations are not defined for constant or unique-constant mode.
... other arithmetical operations ...
==, !=, >, <, >=, and <=. Note, that comparison operations need to be restricted to particular combinations of quantities. For example, temperatures in different scales (thermodynamic, Celsius, etc.) can be compared, while a comparison between a length and a time quantity should be forbidden.... other concepts ...
The Quantities package provides header files and libraries which facilitate to write C++ programs incorporating quantity calculus. This is basically done by defining various types which have built-in abilities to follow and enforce the rules of quantity calculus. Thus, commensurability is tested for numerical and assignment operations, and units are taken into account. Furthermore, other operations are provided (Quantity library). There is also a collection of often used scientific (physical) quantities (see, Physical Quantities) in the PhysicalQuantities library, which is part of Quantities.
Once a C++ program has declared objects with the types mentioned, they can be used to perform quantity calculus. Such an object is generally referred to as a quantity object in the following. The type of such an object is the quantity type. We will further categorize quantity objects by their mode, i.e. whether they refer to a variable, a constant, a unique constant, or an unnamed transient variable.
Unnamed transient quantity objects are often internally created (generated quantity objects), for example as return values of a function. Such objects can be used in operations, but in lieu of a name within the program it is not possible to assign or change the value. Other sources of such quantity objects are certain constructor calls. If this is the constructor of a well-defined quantity, the resulting object carries full unit information. However, generated quantity objects have only limited knowledge about the unit in which the value is stored. In particular, it is assumed that the standardization factor of the unit is 1.0. Thus, generated quantity objects should be used with great care (see below).
In rare cases, dynamic quantity objects are generated and returned from a function. Such an object has a type Dynamic<ST>, where ST is the storage type used (see, Object Types in Quantities (to be finalized)). A dynamic quantity object's properties can not be tested a compile time, since they are only defined at run time. Thus, they are not subject to the usual rules within this package, and could result in errors, which are only detected when the program runs. Consequently, such objects should be avoided as far as possible. At least, they should be converted into or assigned to normal quantity objects as soon as possible after they are returned from a function.
QuantityCluster objects are aggregates of simple quantity objects. In particular, the library implements variable vector, variable tuple, and variable vector tuple objects.
A variable vector object aggregates several variable objects of the same type (homogeneous aggregate). It is intended to avoid some overhead of collecting the various objects in a vector of variable objects.
A variable tuple object aggregates several variable objects of possibly different types (heterogeneous aggregate). It provides an ordered collection of these objects.
A variable vector tuple object aggregates several variable vectors in a certain order.
Quantities, serialization can be used to save the content of a quantity object to a file and later load it into an equivalent object within the same or a separate program run. This is useless for a unique constant, since this has a defined value without the chance to change it.list here further concepts ...
[White_1998] M.A. White, J. Chem. Educ. 75, 607 - 609 (1998).
[BoostMPL] http://www.boost.org/libs/mpl/doc/tutorial/dimensional-analysis.html
[Kernighan/Ritchie_1988] B.W. Kernighan and D.M. Ritchie, The C Programming [Barton/Nackman_1994] J.J. Barton and L.R. Nackman, Scientific and engineering C++: an introduction with advanced techniques and examples, Addison-Wesley, Reading, 1994.
[BoostSerialization] http://www.boost.org/libs/serialization/doc/index.html
[Kernighan/Ritchie_1988] B.W. Kernighan and D.M. Ritchie, The C Programming Language, 2nd edition, Prentice Hall, Engelwood Cliffs, 1988.
[Webster_1993] Webster's Third New International Dictionary, Merriam-Webster, Springfield, 1993.
"[Commensurability_Wikipedia]" http://en.wikipedia.org/wiki/Commensurate
[Dewhurst_2003] S.C. Dewhurst, C++ Gotchas, Addison-Wesley, Boston, 2003.
back to Quantities start page
 1.5.3
1.5.3